# 动手深度学习-Pytorch版

# 前言

目前学习的部分章节，直观地感受是，本书注重于描述模型的抽象结构、以及公式推导。每种模型讲的都不深，但是面面俱到，可以作为机器学习的通识类读物。书中的代码经过验证也都是可运行的，但都是碎片化的案例，可以让学到机器学习程序的基本结构，缺乏工程化的机器学习框架思路。

# 预备知识

# Jupyter Notebook

Jupyter Notebook是一款开源的交互式计算工具，主要用于创建包含实时代码、富文本、数学公式、图表、可视化等内容的文档（文件扩展名为 .ipynb）

使用方法：

下载安装

pip3 install notebook

进入ipynb资源目录，运行notebook

jupyter notebook

打开浏览器，http://localhost:8888/tree

# 如何在conda环境运行jupyter呢？

base 环境安装jupyter

activate base
conda install jupyter jupyterlab

在目标环境安装内核

conda activate myproject
conda install ipykernel # 安装内核
python -m ipykernel install --user --name myproject --display-name "Python (myproject)"  # 注册为jupyter 可选kernel

在base环境运行

jupyter lab  # 功能更丰富的网页端
# 或者
jupyter notebook

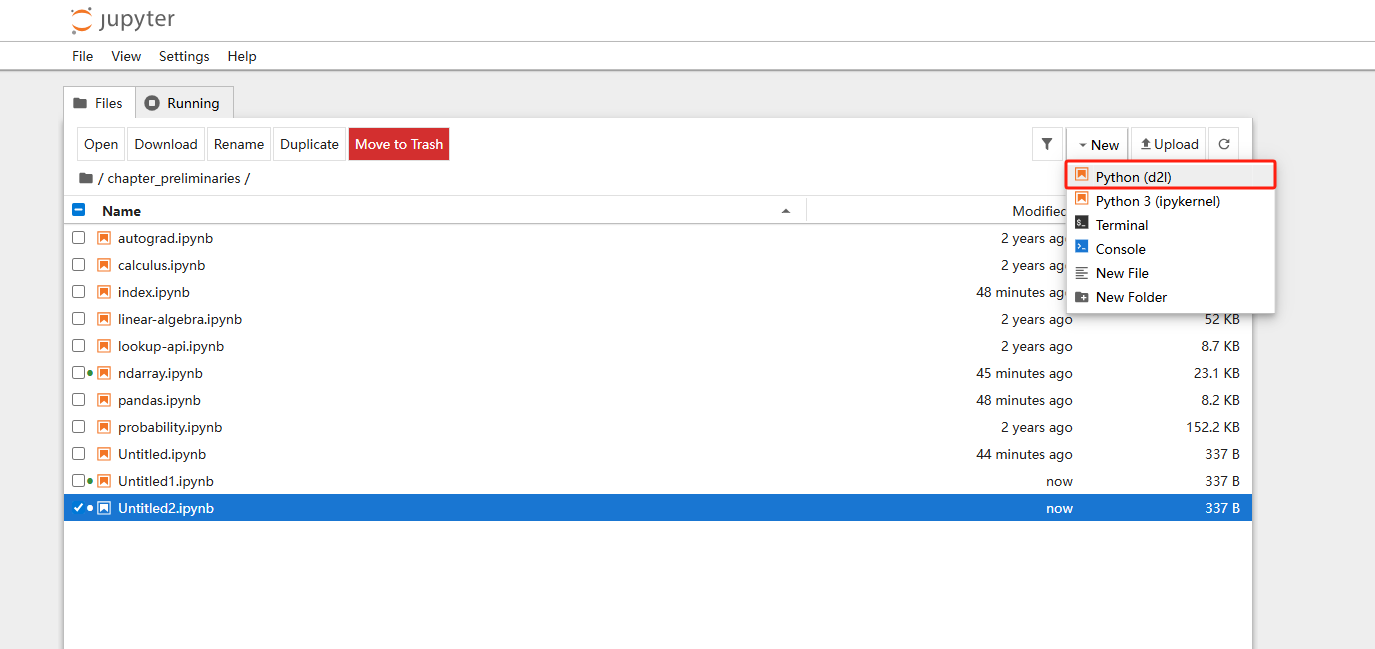
# 数据操作

torch基础操作

x = torch.arange(12)  # 创建张量
x.shape # 查看张量形状
x.numel() # 查看元素数量
    
X = x.reshape(3,4) # 改变张量形状
torch.zeros((2,3,4)) # 用0初始化
torch.ones((2,3,4)) # 用1初始化
torch.randn(3,4) # 用随机数初始化
torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]])  # 用嵌套列表初始化

运算符

常见的标准运算符（+、-、*、/、**）可以升级为按元素运算，

x = torch.tensor([1.0,2,4,8])
y = torch.tensor([2,2,2,2])
x+y,x-y,x*y,x/y,x**y

torch.exp(x) # 包括计算指数


X==Y # 通过逻辑运算符构建张量
X.sum() # 对张量所有元素进行求和

张量连接

X = torch.arange(12,dtype=torch.float32).reshape(3,4)
Y = torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
torch.cat((X,Y),dim=0)  # 沿行的方向拼接
torch.cat((X,Y),dim=1)  # 沿列的方向拼接

广播机制

a = torch.arange(3).reshape(3,1) # a为3行1列
b = torch.arange(2).reshape(1,2) # b为1行2列
a + b # a复制列，b复制行，然后按元素相加

索引和切片

X[-1],X[1:3]  # 最后一个元素， 第二个元素和第三个元素

X[1:2] = 9 # 指定索引来写入矩阵

X[0:2, :] = 12 # 第一行、第二行赋值为12  ：表示沿轴1的所有元素

节省内存

before = id(Y)  # id()获取内存中对象的地址
Y = Y + X  # Y 内存引用地址已经变化
id(Y) == before

原地操作

>>> Z = torch.zeros_like(Y)
>>> id(Z)
2337955335120
>>>
>>> Z[:] = X + Y
>>> id(Z)
2337955335120

>>> before = id(X)
>>> X += Y
>>> id(X) == before
True

转换为其他python对象

torch与numpy数组共享底层内存

>>> A = X.numpy()
>>> B = torch.tensor(A)
>>> type(A),type(B)
(<class 'numpy.ndarray'>, <class 'torch.Tensor'>)

大小为1的张量与Python标量转换

>>> a = torch.tensor([3.5])
>>> a,a.item(),float(a),int(a)
(tensor([3.5000]), 3.5, 3.5, 3)

# 线性代数

标量

import torch

x = torch.tensor(3.0)
y = torch.tensor(2.0)

x + y, x * y, x / y, x**y

向量

x = torch.arange(4)

矩阵

A = torch.arange(20).reshape(5, 4)
A.T

张量

X = torch.arange(24).reshape(2, 3, 4)

# 概率论

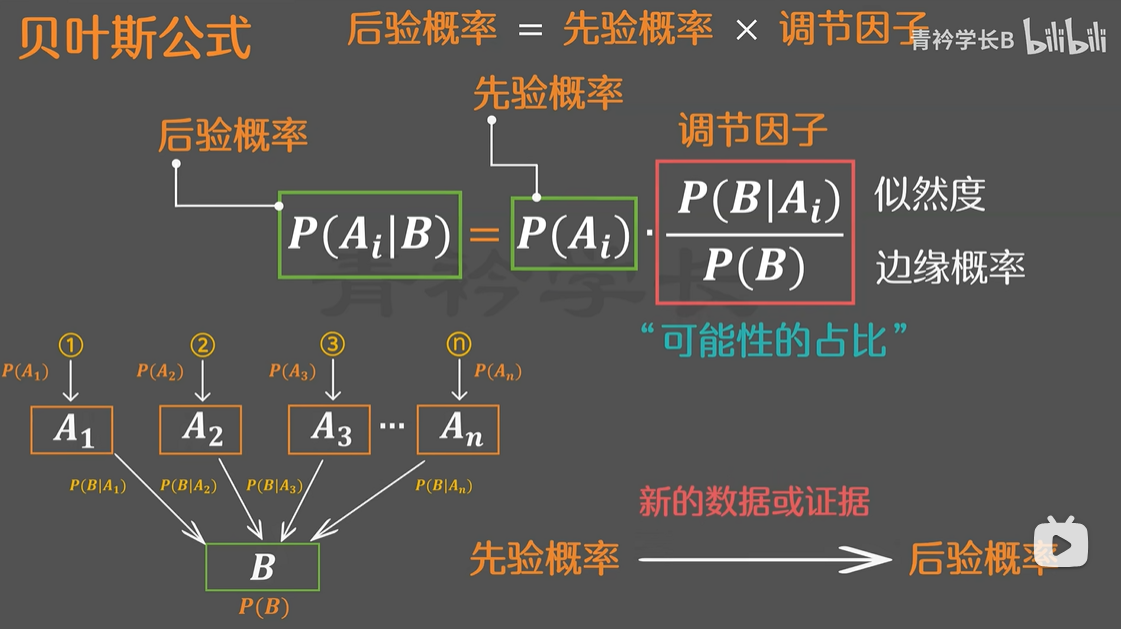
看到103页了

# 线性神经网络

# 多层感知机

# 深度学习计算

# 卷积神经网络

# 现代卷积神经网络

# 循环神经网络（下次看）

循环神经网络（recurrent neural networks,RNNS）,是具有隐状态的神经网络。

隐藏层是在从输入到输出的路径上隐藏的层，隐状态是在给定步骤所做的任何事情的输入，并且这些状态只能拿通过先前时间步的数据来计算。

# 梯度问题

1、梯度爆炸：反向传播过程中，梯度在逐层传递时出现“趋近于无穷大”的极端情况

核心原因：权重矩阵的谱范数（权重值的平均大小）> 1，且激活函数导数的绝对值 ≥ 1

2、梯度消失：反向传播过程中，梯度在逐层传递时出现“趋近于0”的极端情况

核心原因：激活函数导数的绝对值<1，权重矩阵谱范数<=1

3、梯度裁剪：将梯度g投影回给定半径的球

解决方案：

有限使用ReLU及其变体
避免使用sigmoid/tanh（深层网络中）

# 现代循环神经网络

# 门控循环单元GRU

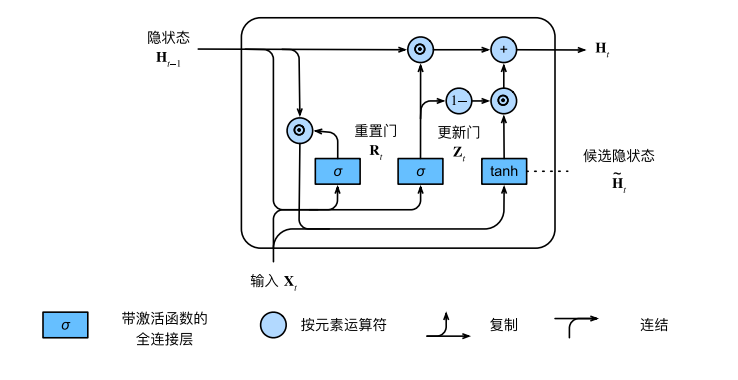
GRU可以更好的捕获时间步距离很长的序列上的依赖关系。

重置门有助于捕获序列中的短期依赖关系。

更新门有助于捕获序列中的长期依赖关系。

重置们打开时，门控循环单元包括基本循环神经网络；更新们打开时，门控循环单元可以跳过子序列。

# 长短期记忆网络LSTM

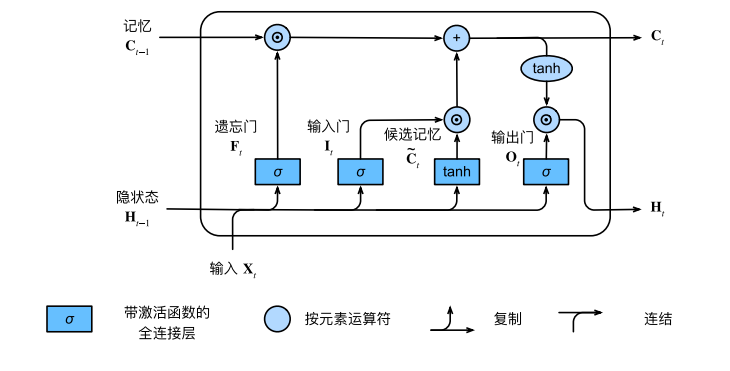
长短期记忆网络有三种类型的门：输入门、遗忘门、输出门。

长短期记忆网络的隐藏层输出包括“隐状态”和“记忆元”。只有隐状态会传递到输出层，而记忆元完全属于内部信息。

长短期记忆网络可以缓解梯度消失和梯度爆炸。

# 深度循环神经网络

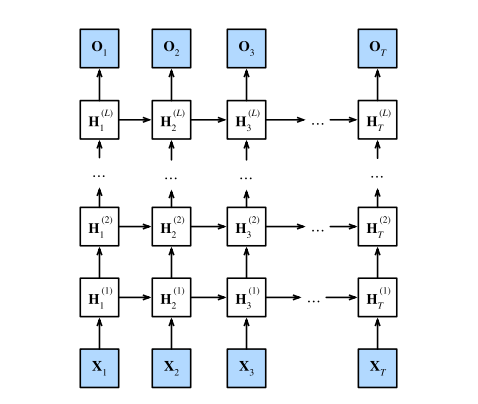
深度循环神经网络中，隐状态的信息北传递到当前层的下一时间步和下一层的当前时间步。

深度循环神经网络需要大量的调参来确保收敛，模型的初始化也需要谨慎。

# 双向循环神经网络

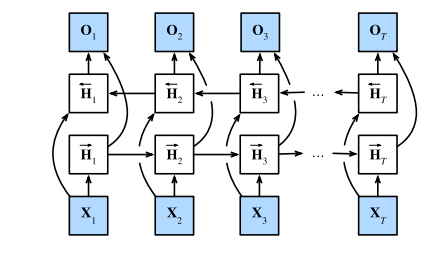
双向循环神经网络，每个时间步的隐状态由当前时间步的前后数据同时决定

双向循环神经网络与概率图模型的“前向-后向”算法具有相似性。

双向循环神经网络主要用于序列编码和给定双向上下文的观测估计。

由于梯度链更长，因此训练代价非常高。

# 机器翻译与数据集

机器翻译是指将序列从一种语言自动翻译成另一种语言。

# 编码器-解码器架构

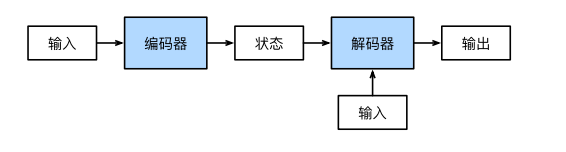
“编码器-解码器”架构可以将长度可变的序列作为输入和输出，因此适用于机器翻译等序列转换问题。

编码器将长度可变的序列作为输入，并将其转换为固定形状的编码状态。

解码器将具有固定形状的编码状态映射为长度可变的序列。

# 序列到序列学习seq2seq

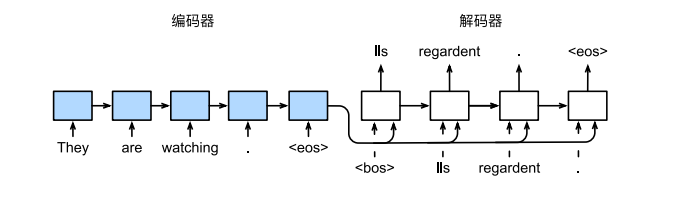
使用RNN-Encoder和RNN-decoder的seq2seq学习

# 注意力机制

具体可参考知乎的一篇文章 (opens new window)

# 注意力提示

非自主性提示是基于环境中物体的突出性和易见性。假如面前有五个物品：一份报纸、一篇研究论文、一杯咖啡、一本笔记本和一本书。所有纸质品都是黑白印刷的，单咖啡杯是红色的。咖啡杯在环境中就会比较显眼，不由自主地引起人们注意。

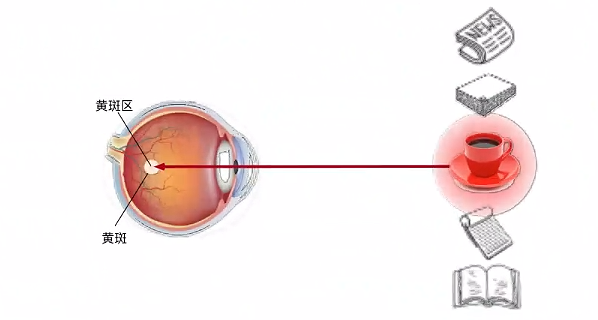
喝咖啡后，我们会变得兴奋并且想读书，所以转过头，重新聚焦眼睛，然后看看书。此时选择书是收到了认知和意识的控制。

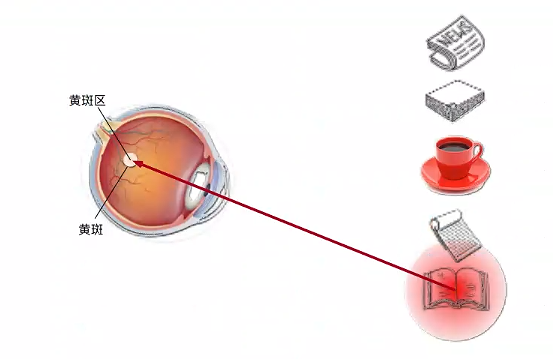
在注意力的背景下，自主性提示被称为查询（query）。给定任何查询，注意力机制通过注意力汇聚，将选择引导至感官输出。在注意力机制中，这些感官输出被称为值（value），每个值与一个**键（key）**对应，可以想象为感官输入的非自主性提示。

注意力机制通过注意力汇聚，将查询（自主性提示）和键（非自主性提示）结合到一起，实现对值的选择倾向。

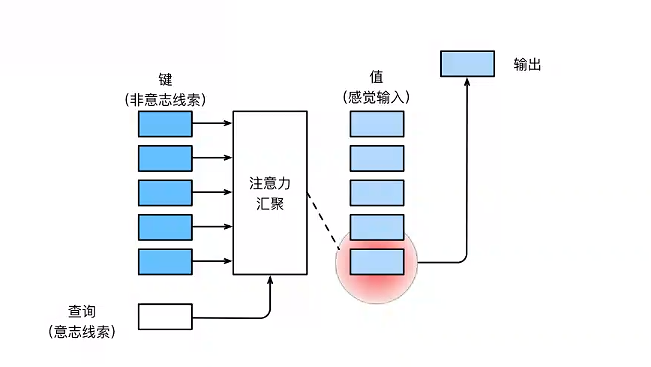
采用平均汇聚：

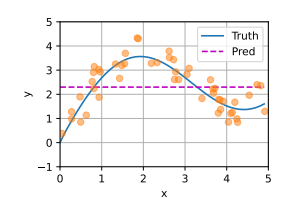
# 注意力汇聚

Nadaraya-Watson核回归模型 $$ f(x) = \sum_{i=1}^{n} \frac{K(x - x_i)}{\sum_{j=1}^{n} K(x - x_j)} y_i, $$ K是核(kernel)，按注意力机制框架重写 $$ f(x) = \sum_{i=1}^{n} \alpha(x, x_i) y_i $$ x是查询,(xi，yi)是键值对，注意力汇聚是yi的加权平均。x和键xi之间的关系建模称为注意力权重。模型的所有键值对注意力权重非负，总和为1.

考虑一个高斯核： $$ K(u) = \frac{1}{\sqrt{2\pi}} \exp(-\frac{u^2}{2}). $$ 带入以上公式得到： $$ f(x) = \sum_{i=1}^{n} \alpha(x, x_{i}) y_{i} = \sum_{i=1}^{n} \frac{\exp(-\frac{1}{2}(x - x_{i})^{2})}{\sum_{j=1}^{n} \exp(-\frac{1}{2}(x - x_{j})^{2})} y_{i} = \sum_{i=1}^{n} \mathrm{softmax}\left(-\frac{1}{2}(x - x_{i})^{2}\right) y_{i}. $$ 如果一个键xi越是接近查询x，那么分配给这个键对应值yi的注意力权重就会越大。

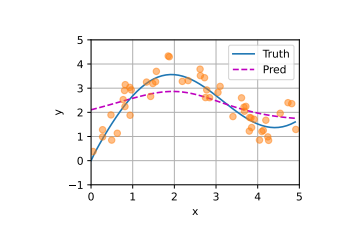
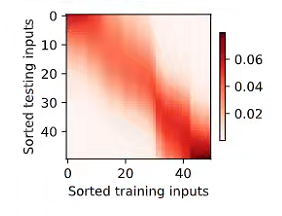
# 注意力评分函数

将注意力汇聚的输出计算可以作为值的加权平均，选择不同的注意力评分函数会带来不同的注意力汇聚操作。

当查询和键是不同长度的矢量时，可以使用加性注意力评分函数。当它们长度相同时，使用缩放点积注意力评分函数计算效率更高

# Bahdanau注意力

# 多头注意力

# Transformer（要重点看）

知乎Transformer介绍文章 (opens new window)

# 阅读进度

目前读到了注意力机制的后半小节，后面需要再看看循环神经网络部分。

← Pytorch学习记录机器学习入门-鱼书 →