# 机器学习入门(鱼书)
本文根据《深度学习入门:基于Python的理论与实现》一书总结,这本书非常适合深度学习入门学习,0基础也可以看懂。
# 神经网络
# MNIST数据集
MNIST数据集是由0-9的数字图像构成的,训练图像有6万张,测试图像有1万张。一般的使用方法是,先用训练图像进行学习,再用学习到的模型度量能在多大程度上对测试图像进行正确的分类。
MNIST图像数据是28像素×28像素的灰度图像(1通道),各个像素取值在0-255之间,每个图像数据都有7、2、1等数字标签。
MNIST数据集用于手写数字识别,可以说是Deep Learning的Hello World!

# 神经网络的学习
# 基本概念
学习的目的是以损失函数为基础,找出能使它的值达到最小的权重参数。实际的神经网络中,参数的数量成千上万,在层数更深的深度学习中,参数的数量可能上亿,想要人工决定这些参数是不可能的,需要用数据来决定。
计算机视觉特征提取算法:
- SIFT(尺度不变特征变换):主打 “尺度 + 旋转不变性”,能在不同大小、旋转角度的图像中找到相同特征,抗光照、噪声能力强,是经典的通用特征提取算法。
- SURF(加速稳健特征):SIFT 的优化版,通过近似计算提升速度,同时保留了尺度和旋转不变性,适合对实时性有要求的场景。
- HOG(方向梯度直方图):专注于 “形状与边缘” 特征,通过统计图像局部区域的梯度方向分布来描述目标轮廓,尤其适合行人检测等刚性目标识别。

机器学习中,一般将数据分为训练数据和测试数据。首先使用训练数据进行学习,寻找最优的参数;然后使用测试数据评价训练的到的模型的实际泛化能力。训练数据也称为监督数据。
仅用一个数据集去学习和评价参数,是无法进行正确评价的。这会导致可以顺利处理某个数据集,但不能处理其他数据集。只对一个数据集过度拟合的状态称为过拟合。
# 损失函数
损失函数是表示神经网络性能好坏的指标,即当前的神经网络对监督数据在多大程度上不拟合,一般用均方误差和交叉熵误差等。
one-hot编码:是一种将离散特征转换为二进制向量的编码方式,核心思想是为每一个唯一的离散值分配一个独立的维度,并用和1表示该特征是否属于某个类别。
假设存在一个离散特征的取值集合为 {A, B, C, D},则每个取值的 one-hot 编码如下:
- A → [1, 0, 0, 0]
- B → [0, 1, 0, 0]
- C → [0, 0, 1, 0]
- D → [0, 0, 0, 1]
均方误差:

交叉熵误差:tk中只有正确解标签的索引为1,单个数据和N个数据的公式如下:


# 梯度下降法
神经网络一般用梯度下降法寻找损失函数的最小值。代码实现求梯度,等同于求多个偏导数,偏导数的计算可以用数值微分解决。
学习率:梯度下降法中控制模型参数更新步长的超参数,决定了每次迭代时模型向最优解靠近的幅度。学习率的选择很重要,过大过小都不行。
神经网络的学习步骤:
- 步骤1:mini-batch 从训练数据中随机选出一部分数据,称为mini-batch,目标是减小损失函数的值
- 步骤2:计算梯度,表示损失函数减小最多的方向
- 步骤3:更新参数:将权重参数沿梯度方向进行微小更新
- 步骤4:重复步骤1、步骤2、步骤3
# 误差反向传播法
反向传播传递“局部倒数”。
计算图中途求得的导数的结果可以被共享,从而可以高效地计算多个导数。
链式法则是关于复合函数的导数的性质。
# 反向传播
反向传播:
- 加法节点的反向传播将上游的值传给下游,不需要正向传播的输入信号。
- 乘法的反向传播将上游的值乘以正向传播的翻转值传递给下游,需要正向传播的输入信号值。

# 激活函数
ReLU激活函数:


SigMod激活函数:


# Affine/Softmax层
- Affine层:对数据进行线性变换+偏置,即仿射变换
- ReLU(Rectified Linear Unit修正线性单元)层:引入非线性,增强网络表达能力
- SoftMax层:将输出转换为概率分布,用于分类决策
配合关系:输入 → Affine 层(线性变换)→ ReLU 层(非线性激活)→ ...(多次重复)→ Affine 层(输出 logits)→ SoftMax 层(输出概率)→ 分类决策
# 与学习相关的技巧
# 参数的更新
SGD随机梯度下降法:如果函数形状呈延伸状,搜索路径就会比较低效

Momentum:考虑到速度,加速SGD

AdaGrad:为不同的参数自适应调整学习率,会记录过去所有梯度的平方和。(RMSProp方法会遗忘过去的参数,窗口滑动平均)

Adam:融合了Momentum和AdaGrad方法,学习的更新程度被适当调整
- 计算参数梯度的一阶矩估计(类似动量,积累梯度的指数移动平均,反映梯度的方向趋势);
- 计算参数梯度的二阶矩估计(类似 RMSprop,积累梯度平方的指数移动平均,反映梯度的尺度信息);
- 对这两个矩估计进行偏差修正(解决初始阶段估计偏差问题);
- 基于修正后的矩估计,动态调整每个参数的学习率,实现自适应更新。
# 权重的初始值
梯度消失:偏向0和1的数据分布会造成反向传播中的梯度值不断变小,最后消失。
表现力受限:激活值在分布上有所偏向

# 卷积神经网络
# 整体结构
卷积神经网络(Convolutional Neural Network,CNN)
全连接:相邻层的所有神经元都有连接
一个5层的全连接的神经网络结构如下图:
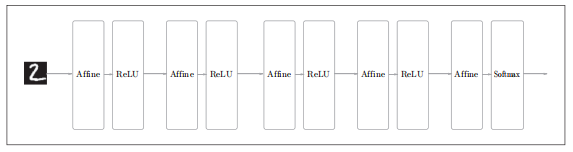
使用CNN会是什么样子呢?
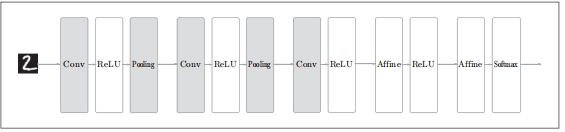
Affine-ReLU层被替换为Convolution-RElu-(Pooling)
# 卷积层
全连接层忽视了数据的形状,例如图像是包含长、宽、通道的三维数据
卷积层的输入输出称为特征图,卷积层的输入数据称为输入特征图,卷积层的输出数据称为输出特征图
CNN中,滤波器的参数对应之前的权重
填充:在进行卷积层的处理之前,有时要向输入数据的周围填充固定的数据,比如0
步幅:应用滤波器的位置间隔
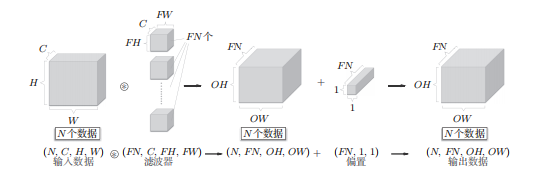
输出大小的计算:输入大小为(H,W),滤波器大小为(FH,FW),输出大小为(OH,OW),填充为P,步幅为S
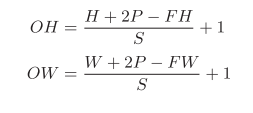
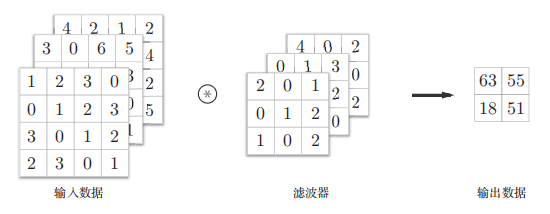
3维数据的卷积运算:通道方向上有多个特征图是,会按通道进行数据和滤波器的卷积运算,将结果叠加输出
批处理:
# 池化层
池化是缩小高、长方向上的空间的运算。
池化层没有要学习的参数,通道数不发生变化,池化操作是按通道独立进行的。对微小的位置变化具有稳健性。
CNN各层间传递的是4维数据。
im2col函数:将卷积操作转化为矩阵乘法
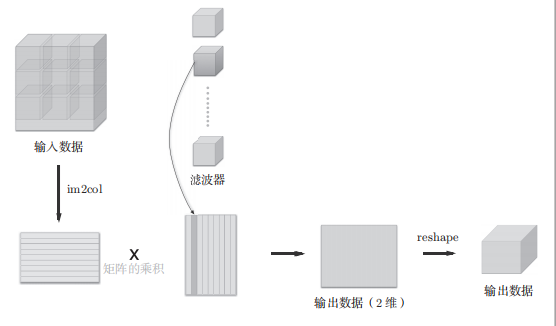
左侧矩阵(A×B),A是有多少个卷积窗口,B是一个卷积窗口内有多少个元素(可扩展到N个数据)
右侧矩阵(C×D),C是一个卷积核内有多少个元素,D是卷积核的数量
输出数据(A×D),每一列可复原为一个二维矩阵

# CNN的可视化
CNN学习前和学习后卷积核的比较

AlexNet
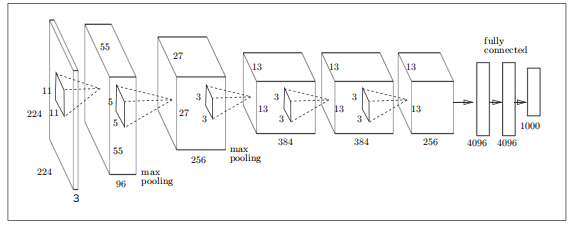
# 深度学习
深度学习是加深了层的深度神经网络
# 加深网络
集成学习、学习率衰减、Data Augmentation(数据扩充)等都有助于提高识别精度。
数据扩充:人为的通过旋转、平移等微小变化,增加图像数量

加深层的一个好处是可以减少网络参数的数量
# 加深学习的小历史
ImageNet是拥有超过100万张图像的数据集,并且每张图像都被关联了标签。每年都会举办使用这个巨大数据集的ILSCRC图像识别大赛。
VG、GoogleNet、ResNet
# 深度学习的高速化
GPU不仅用于图像处理,也用于通用的数值计算。深度学习中需要进行大量的乘积累加运算,或者大型矩阵的乘积运算,对这种大量的并行运算正式GPU所擅长的。
GPU主要有NVIDIA和AMD两家公司提供,但是大多数深度学习框架只受益于NNVIDIA的GPU,因为深度学习框架中使用了NVIDIA提供的CUDA这个面向GPU计算的综合开发环境。
分布式学习框架:Google的TensorFlow、微软的CNTK
深度学习中,16位的半精度浮点数,也可以顺利进行学习。
# 深度学习的应用
物体的检测:从图像中确定物体位置,并进行分类
图像分割:在像素水平对图像进行分类
图像标题的生成
RNN(Recurrent Neural Network)是呈递归式连接的网络,经常被用于自然语言、时间序列数据的连续性数据上。NIC组合了CNN和RNN,可以生成惊人的高精度图像标题。
# 深度学习的未来
图像风格变换:风格迁移
图像生成:DCGAN( Deep Convolutional Generative Adversarial Networks)深度卷积生成对抗网络、GAN(Generative Adversarial Networks)生成对抗网络
DCGAN使用了深度学习,技术要点是使用了生成者Generatpr生成近似真品的图像,使用识别者Discriminator判别是不是真图像。两者以竞争方式学习。
监督学习与无监督学习,数据集中的标签就属于监督数据。
自动驾驶
强化学习:代理(Agent)根据环境选择行动,然后通过行动改变环境。
# 报错解决
# Pycharm中使用matplotlib可视化数据时
AttributeError: 'FigureCanvasInterAgg' object has no attribute 'tostring_rgb'. Did you mean: 'tostring_argb'?
在Pycharm设置中的Tools->Python Plots取消下面两个选项就可解决

目前学习到240页