# LearnOpenGL-06PBR
# PBR材质
PBR,是指基于物理的渲染(Physically Based Rendering),它指的是基于与现实世界的物理原理更相符的渲染技术的集合。
# 微平面模型
微平面理论认为达到微观尺度后任何平面都可以用微平面的细小镜面来描绘。

粗糙度:用统计学的方法估计微平面的粗糙程度。粗糙度通常记为α,范围0-1。
半程向量h:光线向量l和视线向量v之间的单位化中间向量。 $$ h = \frac{l + v}{|l + v|} $$ 微平面的朝向方向与半程向量的方向越是一致,镜面反射的效果就越是强烈越是锐利。粗糙度越高,镜面反射的轮廓越大。

# 能量守恒
反射光线和折射光线的能量总和不会超过入射光线。
float kS = calculateSpecularComponent(...); // 反射/镜面 部分
float kD = 1.0 - ks; // 折射/漫反射 部分
反射率方程:表示从观察方向上观察,光线投射到点p上反射出的辐射率的总和。 $$ L_o(p,\omega_o) = \int\limits_{\Omega} f_r(p,\omega_i,\omega_o) L_i(p,\omega_i) n \cdot \omega_i d\omega_i $$ 辐射率被用来量化来自单一方向上的光线的大小或者强度。
辐射通量:辐射通量Φ表示的是一个光源所输出的能量,以瓦特为单位。
立体角:立体角用ω表示,它可以为我们描述投射到单位球体上的一个截面的大小或者面积。
辐射强度:辐射强度(Radiant Intensity)表示的是在单位球面上,一个光源向每单位立体角所投送的辐射通量。
计算辐射强度: $$ I = \frac{d\Phi}{d\omega} $$ 辐射照度:当涉及到辐射率时,我们通常关心的是所有投射到点p上的光线的总和,而这个和就称为辐射照度或者辐照度
# BRDF
双向反射分布函数BRDF:可以近似的求出每束光线对一个给定了材质属性的平面上最终反射出来的光线所作出的贡献程度。
Cook-Torrance BRDF兼有漫反射和镜面反射两个部分: $$ f_r = k_d f_{lambert} + k_s f_{cook-torrance} $$ 漫反射部分:对表面颜色进行标准化 $$ f_{lambert} = \frac{c}{\pi} $$ 镜面反射部分: $$ f_{cook-torrance} = \frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)} $$
分子是三个函数:
- 法线分布函数:估算在受到表面粗糙度的影响下,朝向方向与半程向量一致的微平面的数量。这是用来估算微平面的主要函数。
- 几何函数:描述了微平面自成阴影的属性。当一个平面相对比较粗糙的时候,平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。
- 菲涅尔方程:菲涅尔方程描述的是在不同的表面角下表面所反射的光线所占的比率。
D使用Trowbridge-Reitz GGX,F使用Fresnel-Schlick近似(Fresnel-Schlick Approximation),而G使用Smith’s Schlick-GGX。
# 法线分布函数
法线分布函数D,从统计学上近似的表示了与半程向量h取向一致的微平面的比率。 $$ NDF_{GGX TR}(n, h, \alpha) = \frac{\alpha^2}{\pi((n \cdot h)^2 (\alpha^2 - 1) + 1)^2} $$ α是粗糙度,h是半程向量,n是法线方向。
# 几何函数
几何函数从统计学上近似求得微平面间相互遮挡的比率,这种遮挡会损耗光线能量。
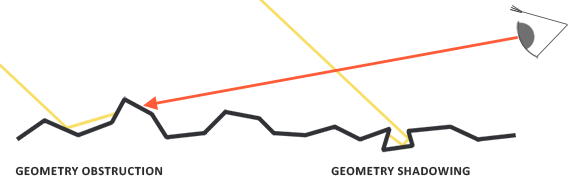
几何函数采用一个材料的粗糙度参数作为输入参数,粗糙度较高的表面其微平面间相互遮蔽的概率就越高。 $$ G_{SchlickGGX}(n, v, k) = \frac{n \cdot v}{(n \cdot v)(1 - k) + k } $$ k是α的重映射,分为直接光照和针对IBL光照。
几何函数是一个值域为[0.0, 1.0]的数,其中白色或者说1.0表示没有微平面阴影,而黑色或者说0.0则表示微平面彻底被遮蔽。
# 菲涅尔方程
菲涅尔(发音为Freh-nel)方程描述的是被反射的光线对比光线被折射的部分所占的比率,这个比率会随着我们观察的角度不同而不同。 $$ F_{Schlick}(h, v, F_0) = F_0 + (1 - F_0) ( 1 - (h \cdot v))^5 $$ F0表示平面的基础反射率
电介质材质表面的基础反射率不高于0.17。
金属材质表面反射率在0.5-1.0之间。
金属表面基础反射率是带有色彩的,反射率与波长有关。
金属度用来描述一个材质表面是金属还是非金属的。
# Cook-Torrance反射率方程
$$ L_o(p,\omega_o) = \int\limits_{\Omega} (k_d\frac{c}{\pi} + k_s\frac{DFG}{4(\omega_o \cdot n)(\omega_i \cdot n)})L_i(p,\omega_i) n \cdot \omega_i d\omega_i $$
# 编写PBR材质
在下面你可以看到在一个PBR渲染管线当中经常会碰到的纹理列表,还有将它们输入PBR渲染器所能得到的相应的视觉输出:

PBR材质包含的纹理贴图:
- 反照率:为每个金属的纹理像素指定表面颜色或者基础反射率。
- 法线:为表面制造出凹凸不平的效果。
- 金属度:指定每个纹理像素是不是金属质地的。
- 粗糙度:指定某个表面有多粗糙。
- AO:环境光遮蔽为表面和周围潜在的几何图形指定了额外的阴影因子。